Geometrical Formulation of Yield Surfaces

Yield functions are commonly visualized as surfaces in the principal stress space, centered around the hydrostatic axis. According to the von Mises yield criterion, the yield surface takes the shape of a cylinder. However, it is not always immediately clear how the mathematical form of this criterion results in a cylindrical surface. In this post, the geometrical formulation of the von Mises yield criterion will be derived step by step.

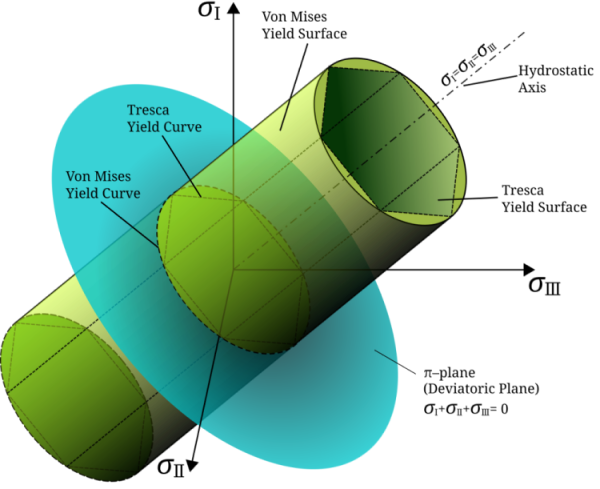Ref: Wikipedia, Von Misses Yield Criterion

\[\sigma_{\text{VM}} = \sqrt{\frac{1}{2} \left[ (\sigma_1 - \sigma_2)^2 + (\sigma_2 - \sigma_3)^2 + (\sigma_1 - \sigma_3)^2 \right]}\]

Let us begin with the basics. A circle is defined as the set of points that are equidistant from a central point. Similarly, a cylinder is the set of points that are equidistant from a central axis.

Assume that the central axis of the cylinder is defined by the line extending from the origin $(0, 0, 0)$ to the point $(1, 1, 1)$. Any point lying on this line can be expressed as $(x, y, z) = (c, c, c)$, where c is a scalar that determines the position along the line. The distance r between any arbitrary point in space and this line can be calculated as follows: \[r^2 = (x - c)^2 + (y - c)^2 + (z - c)^2\]

The shortest distance between a point and a line is the perpendicular distance, which can be determined by minimizing the distance function. This is typically achieved by taking the derivative of the squared distance with respect to the position along the line and solving for the minimum. \[\frac{d(r^2)}{dc} = 2(x - c) + 2(y - c) + 2(z - c) = 0\]

This expression can be further simplified and rearranged as follows: \[x + y + z = 3c\]

By combining these equations, we obtain the following expression: \[r^2 = \left( x - \frac{x + y + z}{3} \right)^2 + \left( y - \frac{x + y + z}{3} \right)^2 + \left( z - \frac{x + y + z}{3} \right)^2\]

This equation can be reformulated in the following form: \[3r^2 = (x - y)^2 + (y - z)^2 + (z - x)^2\]

This is the equation of a cylinder with radius r around the vector $\{1, 1, 1\}$. Any cross-section of the cylinder, taken perpendicular to this axis, is a circle lying on the plane defined by $x+y+z=3c$. Recall that the general equation of a plane in three-dimensional space, passing through the point $(x_0, y_0, z_0)$ with a surface normal vector $\mathbf{n} = \{ n_1, n_2, n_3 \}$ is given by: \[n_1 (x - x_0) + n_2 (y - y_0) + n_3 (z - z_0) = 0\]

Now, it is time to apply this formulation to the principal stress space. The von Mises yield criterion can be expressed in a similar form as follows: \[3 \left( \sqrt{\frac{2}{3}} \sigma_{\text{yield}} \right)^2 = (\sigma_1 - \sigma_2)^2 + (\sigma_2 - \sigma_3)^2 + (\sigma_1 - \sigma_3)^2\]

This equation demonstrates that the yield surface takes the form of a cylinder with a radius of $\sqrt{\frac{2}{3}} \sigma_{\text{yield}}$ , centered around the hydrostatic axis where $\sigma_1 = \sigma_2 = \sigma_3$. Any cross-section of this cylinder, taken perpendicular to the hydrostatic axis, will be described by the following equation: \[\sigma_1 + \sigma_2 + \sigma_3 = 3 I_1\]

Where $I_1$ is the first invariant of the stress tensor. These cylindrical surfaces indicate that there are different levels of hydrostatic stress along the central axis. The elastic region is defined by circular cross-sections with same radius, each corresponding to a different hydrostatic stress level. This demonstrates that the yield behavior of materials is independent of hydrostatic stress.

The same equation can also be expressed in the deviatoric principal stress space, which is defined as: \[\left( \sqrt{\frac{2}{3}} \sigma_{\text{yield}} \right)^2 = s_1^2 + s_2^2 + s_3^2\]

In deviatoric principal space, the yield surface transforms into a sphere with radius $\sqrt{\frac{2}{3}} \sigma_{\text{yield}}$ , centered at the origin.