Octahedral Shear Stress Yield Criterion
Octahedral Stress
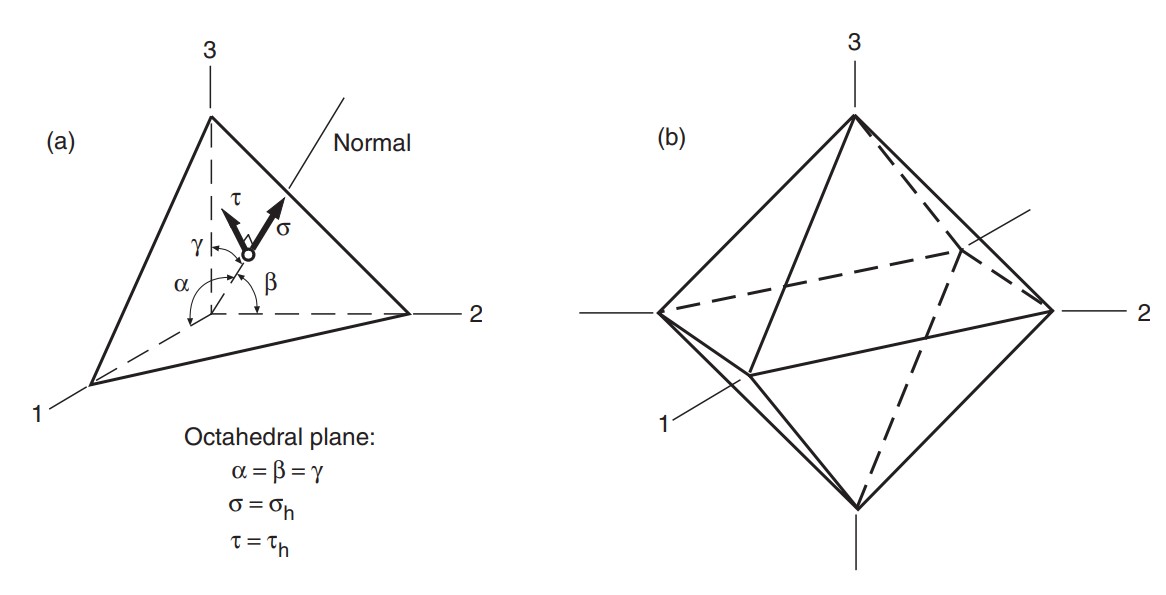
A cross-sectional plane is shown in the figure relative to the principal axes. Normal stress σ and shear stress τ on this plane can be calculated by using the stress tensor and normal vector. The direction of the normal to the cross-sectional plane is characterized by the angles α, β, and γ relative to the principal axes.
 Ref: Dowling, N.E., Mechanical Behavior of Materials
Ref: Dowling, N.E., Mechanical Behavior of Materials
\[\mathbf{T} = [\sigma] \mathbf{n}\]
The cross-sectional plane with equal distance to all principal axes from the origin is referred to as the octahedral plane. The normal stress acting on this plane corresponds to the hydrostatic component of the stress tensor. \[\sigma_{\text{oct}} = \frac{\sigma_1 + \sigma_2 + \sigma_3}{3}\]
The shear stress acting on this plane is responsible of the material’s yielding. \[\tau_{\text{oct}} = \frac{1}{3} \sqrt{(\sigma_1 - \sigma_2)^2 + (\sigma_2 - \sigma_3)^2 + (\sigma_1 - \sigma_3)^2}\]
There are eight octahedral planes, and the normal and shear stresses acting on all these planes are identical. The octahedral normal and shear stresses can also be calculated by using stress invariants. \[\sigma_{\text{oct}} = \frac{I_1}{3}\] \[\tau_{\text{oct}} = \sqrt{\frac{2}{3} J_2}\]
These quantities can be computed directly from stress components, without the need for principal stress calculations. \[\sigma_{\text{oct}} = \frac{\sigma_{11} + \sigma_{22} + \sigma_{33}}{3}\] \[\tau_{\text{oct}} = \frac{1}{3} \sqrt{(\sigma_{11} - \sigma_{22})^2 + (\sigma_{22} - \sigma_{33})^2 + (\sigma_{11} - \sigma_{33})^2 + 6(\sigma_{12}^2 + \sigma_{23}^2 + \sigma_{13}^2)}\]
Material yielding occurs when the octahedral shear stress reaches a critical value. This condition is equivalent to the Von Mises Yield Criterion, as this threshold corresponds to the octahedral shear stress of a uniaxial tension specimen at the yielding point. The advantage of octahedral shear stress over Von Mises stress is that it is defined in a specific direction, whereas Von Mises stress is a scalar quantity. This directional definition is useful when assessing the stress and plasticity of a body in a particular critical direction under a complex load history. \[\tau_{\text{oct}} > \frac{\sqrt{2}}{3} \sigma_{\text{yield}}\]
Consider the following stress tensor: \[[\sigma] = \begin{bmatrix} 100 & 50 & 30 \\ 50 & 150 & 40 \\ 30 & 40 & 120 \end{bmatrix}\]
The principal stresses can be determined by solving the eigenvalue problem of the stress tensor: \[\mathbf{T} = [\sigma] \mathbf{n} = \lambda \mathbf{n}\]
The matrix [V] contains the eigenvectors as its columns, while [Λ] is a diagonal matrix composed of the corresponding eigenvalues. The eigenvectors define the principal directions, and the eigenvalues represent the principal stresses. \[[V] = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} , \quad [\Lambda] = \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & \sigma_3 \end{bmatrix}\]
The stresses acting on octahedral planes result can be obtained by calculating the shear and normal stresses in the eigenbasis, in the direction {1,1,1}. \[[\sigma] = \begin{bmatrix} 208.8 & 0 & 0 \\ 0 & 92.7 & 0 \\ 0 & 0 & 68.4 \end{bmatrix}\] Matlab/Octave Code for Octahedral Stress Calculations
%INPUTS....................................................................
% This code visualizes the traction vector and principal directions of a
% stress tensor. It calculates the normal and shear stresses on a plane.
%..........................................................................
%INPUTS....................................................................
S=[208.8557 0 0; 0 92.7286 0; 0 0 68.4157]; %tensor in principal basis
n=[1 1 1]';
%..........................................................................
%..........................................................................
%#ok<*NOPTS>
%calculate traction vector-------------------------------------------------
n=n/norm(n); %convert the normal vector to unit vector
T=S*n;
f1=figure;
figure(f1)
plot3([0 T(1,1)/norm(T)],[0 T(2,1)/norm(T)],[0 T(3,1)/norm(T)],...
"k","LineWidth",2)
hold on
text(1.15*T(1,1)/norm(T),1.15*T(2,1)/norm(T),1.15*T(3,1)/norm(T),...
'T','FontSize',14,'color', 'k','FontWeight', 'bold')
%--------------------------------------------------------------------------
%calculate normal ans shear stress on the plane----------------------------
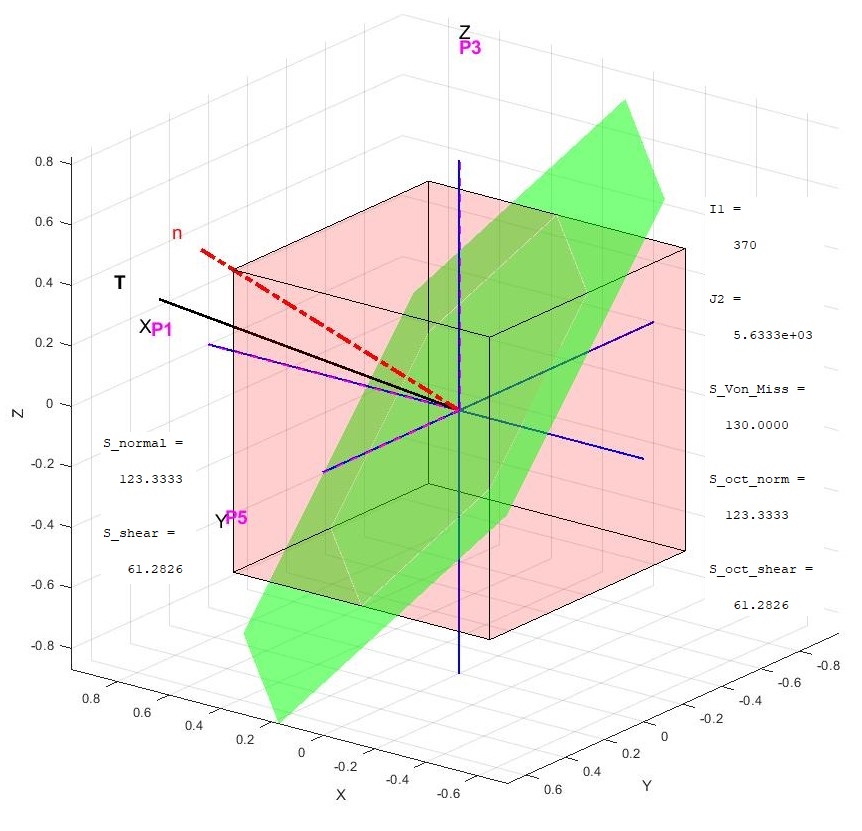
S_normal=T'*n
S_shear=sqrt(norm(T)^2-S_normal^2)
%--------------------------------------------------------------------------
%calculate and plot principal directions-----------------------------------
[V,L]=eig(S);%calculate principal stresses and directions
B=diag(L);
[C,I] = sort(B,'descend');%sort eigenvalues
Prin_Stress=diag(C)
Prin_Direct=V(:,I)
V=Prin_Direct;
plot3([0 V(1,1)],[0 V(2,1)],[0 V(3,1)],"--m","LineWidth",2)
plot3([0 V(1,2)],[0 V(2,2)],[0 V(3,2)],"--m","LineWidth",2)
plot3([0 V(1,3)],[0 V(2,3)],[0 V(3,3)],"--m","LineWidth",2)
text(1.2*V(1,1),1.2*V(2,1),1.2*V(3,1),...
'P1','FontSize',14,'color', 'm','FontWeight', 'bold')
text(1.2*V(1,2),1.2*V(2,2),1.2*V(3,2),...
'P5','FontSize',14,'color', 'm','FontWeight', 'bold')
text(1.2*V(1,3),1.2*V(2,3),1.2*V(3,3),...
'P3','FontSize',14,'color', 'm','FontWeight', 'bold')
%--------------------------------------------------------------------------
%plot mohrs circle---------------------------------------------------------
p12 = nsidedpoly(1000,'Center',[0.5*(Prin_Stress(1,1)+Prin_Stress(2,2))...
0], 'Radius', 0.5*abs(Prin_Stress(1,1)-Prin_Stress(2,2)));
p13 = nsidedpoly(1000,'Center',[0.5*(Prin_Stress(1,1)+Prin_Stress(3,3))...
0], 'Radius', 0.5*abs(Prin_Stress(1,1)-Prin_Stress(3,3)));
p23 = nsidedpoly(1000,'Center',[0.5*(Prin_Stress(2,2)+Prin_Stress(3,3))...
0], 'Radius', 0.5*abs(Prin_Stress(2,2)-Prin_Stress(3,3)));
f2=figure;
figure(f2)
plot(p12, 'FaceColor', 'r')
hold on
plot(p13, 'FaceColor', 'g')
plot(p23, 'FaceColor', 'b')
grid on
text(Prin_Stress(1,1),0,['P1:' newline num2str(round(Prin_Stress(1,1),1))],...
'FontSize',14,'color','m','FontWeight','bold')
text(Prin_Stress(2,2),0,['P2:' newline num2str(round(Prin_Stress(2,2),1))],...
'FontSize',14,'color','m','FontWeight','bold')
text(Prin_Stress(3,3),0,['P3:' newline num2str(round(Prin_Stress(3,3),1))],...
'FontSize',14,'color','m','FontWeight','bold')
text(0.5*(Prin_Stress(2,2)+Prin_Stress(3,3)),0.5*abs(Prin_Stress(1,1)-...
Prin_Stress(3,3)),['Max Shear:' num2str(round(0.5*abs(Prin_Stress(1,1)-...
Prin_Stress(3,3)),1))],'FontSize',14,'color','m','FontWeight','bold')
axis equal
plot([Prin_Stress(3,3) 1.1*Prin_Stress(1,1)],[0 0],'k')
text(1.12*Prin_Stress(1,1),0,'S_n','FontSize',14)
plot([Prin_Stress(3,3) Prin_Stress(3,3)],[-0.55*abs(Prin_Stress(1,1)-...
Prin_Stress(3,3)) 0.55*abs(Prin_Stress(1,1)-Prin_Stress(3,3))],'k')
text(Prin_Stress(3,3),0.57*abs(Prin_Stress(1,1)-Prin_Stress(3,3)),...
'S_s','FontSize',14)
%--------------------------------------------------------------------------
%calculate I1--------------------------------------------------------------
I1=sum(diag(L))
%--------------------------------------------------------------------------
%Calculate J2--------------------------------------------------------------
J2=1/6*((L(1,1)-L(2,2))^2+(L(2,2)-L(3,3))^2+(L(1,1)-L(3,3))^2)
%--------------------------------------------------------------------------
%Calculate Von Misses Stress-----------------------------------------------
S_Von_Miss=sqrt(3*J2)
%--------------------------------------------------------------------------
%Calculate Octahedral Stress-----------------------------------------------
S_oct_norm=I1/3
S_oct_shear=sqrt(2/3*J2)
%--------------------------------------------------------------------------
%draw a unit cube centered at coordinate origin----------------------------
%this part of the code is only for visualization---------------------------
cube_corners= [...
-0.5 -0.5 -0.5;
0.5 -0.5 -0.5;
0.5 0.5 -0.5;
-0.5 0.5 -0.5;
-0.5 -0.5 0.5;
0.5 -0.5 0.5;
0.5 0.5 0.5;
-0.5 0.5 0.5];
xc = cube_corners(:,1);
yc = cube_corners(:,2);
zc = cube_corners(:,3);
idx = [1 2 3 4 1; 5 6 7 8 5; 1 2 6 5 1; 4 3 7 8 4; 2 3 7 6 2;1 4 8 5 1]';
figure(f1)
patch(xc(idx),yc(idx),zc(idx),'r', 'facealpha', 0.1)
xlabel('X')
ylabel('Y')
zlabel('Z')
view(3)
grid on
axis equal
hold on
plot3([-1.15 1.15],[0 0],[0 0],"b","LineWidth",1.5)
plot3([0 0],[-1.15 1.15],[0 0],"b","LineWidth",1.5)
plot3([0 0],[0 0],[-1.15 1.15],"b","LineWidth",1.5)
txt = '\leftarrow sin(\pi) = 0';
text(1.25,0,0,'X','FontSize',14)
text(0,1.25,0,'Y','FontSize',14)
text(0,0,1.25,'Z','FontSize',14)
xlim([-2 2])
ylim([-2 2])
zlim([-2 2])
%--------------------------------------------------------------------------
%draw the unit normal of the cross section---------------------------------
plot3([0 n(1,1)],[0 n(2,1)],[0 n(3,1)],"-.r","LineWidth",3)
text(1.1*n(1,1),1.1*n(2,1),1.1*n(3,1),'n','FontSize',14,'color', 'r')
%--------------------------------------------------------------------------
%draw a plane normal to n and passing through origin (0,0,0)---------------
%a plane is a*x+b*y+c*z+d=0 >>>>[a,b,c] is the normal
if n(3,1)==0
if n(1,1)==0
[xx,zz]=ndgrid(-0.75:0.5:0.75,-0.75:0.5:0.75);%create a grid
yy=0*xx;
elseif n(2,1)==0
[yy,zz]=ndgrid(-0.75:0.5:0.75,-0.75:0.5:0.75);%create a grid
xx=0*yy;
else
[yy,zz]=ndgrid(-0.75:0.5:0.75,-0.75:0.5:0.75);%create a grid
xx=(-n(2,1)/n(1,1))*yy;
end
else
[xx,yy]=ndgrid(-0.75:0.5:0.75,-0.75:0.5:0.75);%create a grid
zz=(-1/n(3,1))*(n(1,1)*xx+n(2,1)*yy);
end
surf(xx,yy,zz,'FaceAlpha',0.5,'EdgeColor', 'none', 'FaceColor', 'g')
%--------------------------------------------------------------------------
The output of the code is provided below. It is important to note that the shear stresses are calculated using vector rotation and stress invariants, with both methods yielding identical results, as expected. You are encouraged to modify the normal direction to other octahedral planes, such as (1, -1, 1), and observe that the normal and shear stresses remain the same across all octahedral planes.