Derivation of Cylindrical Yield Surface
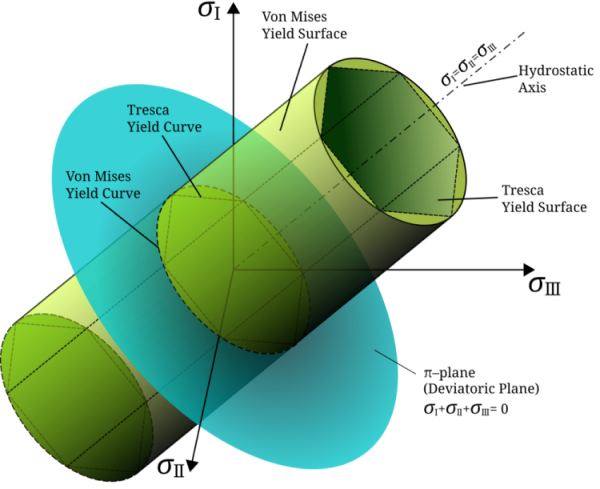 Yield functions are commonly visualized as surfaces in the principal stress space, centered around the hydrostatic axis. According to the von Mises yield criterion, the yield surface takes the shape of a cylinder. However, it is not always immediately clear how the mathematical form of this criterion results in a cylindrical surface. In this post, the geometrical formulation of the von Mises yield criterion will be derived step by step. Read More ›
Yield functions are commonly visualized as surfaces in the principal stress space, centered around the hydrostatic axis. According to the von Mises yield criterion, the yield surface takes the shape of a cylinder. However, it is not always immediately clear how the mathematical form of this criterion results in a cylindrical surface. In this post, the geometrical formulation of the von Mises yield criterion will be derived step by step. Read More ›
Octahedral Shear Stress Yield Criterion
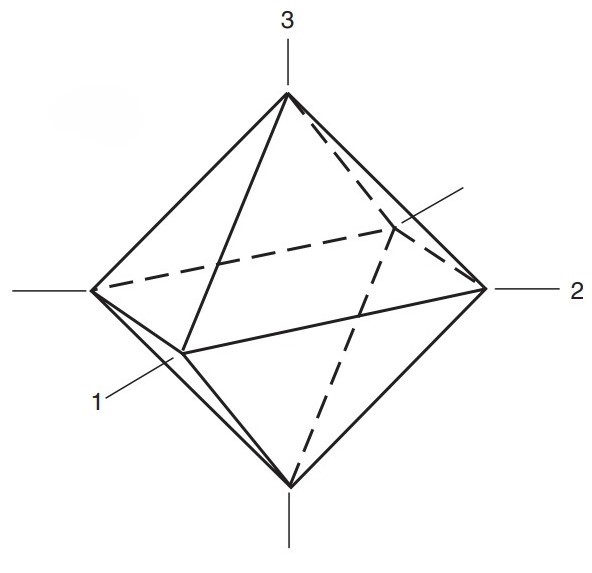 The cross-sectional plane with equal distance to all principal axes from the origin is referred to as the octahedral plane. There are eight octahedral planes, and the normal and shear stresses acting on all these planes are identical. The shear stress acting on this plane is responsible of the material’s yielding. Read More ›
The cross-sectional plane with equal distance to all principal axes from the origin is referred to as the octahedral plane. There are eight octahedral planes, and the normal and shear stresses acting on all these planes are identical. The shear stress acting on this plane is responsible of the material’s yielding. Read More ›
Maximum Shear Stress
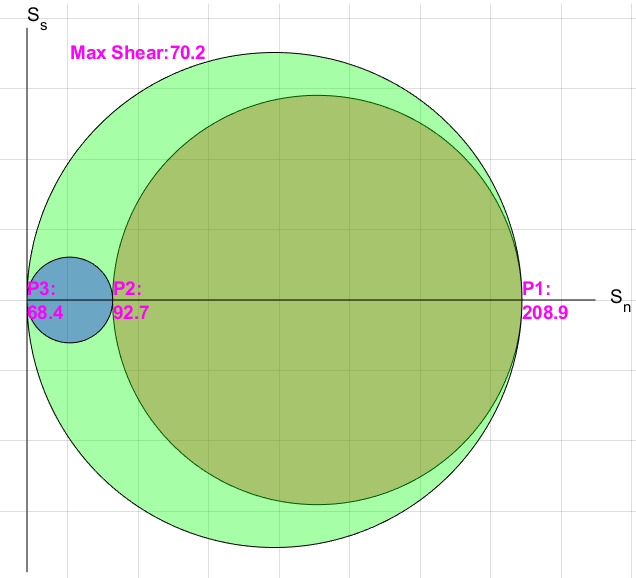 Mohr’s circle provides a two-dimensional graphical representation of the transformation laws for the Cauchy stress tensor. It allows the graphical determination of the stress components acting on a rotated plane passing through the same point. Read More ›
Mohr’s circle provides a two-dimensional graphical representation of the transformation laws for the Cauchy stress tensor. It allows the graphical determination of the stress components acting on a rotated plane passing through the same point. Read More ›
Cauchy's Stress Theorem
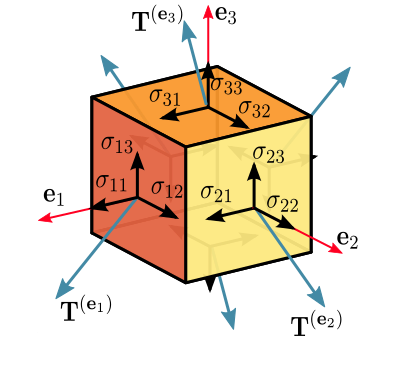 The stress tensor and its properties provide an ideal starting point for an engineering blog focused on solid mechanics. A solid understanding of this tensor facilitates comprehension of concepts such as coordinate transformation, principal stress, and yield criteria. Read More ›
The stress tensor and its properties provide an ideal starting point for an engineering blog focused on solid mechanics. A solid understanding of this tensor facilitates comprehension of concepts such as coordinate transformation, principal stress, and yield criteria. Read More ›